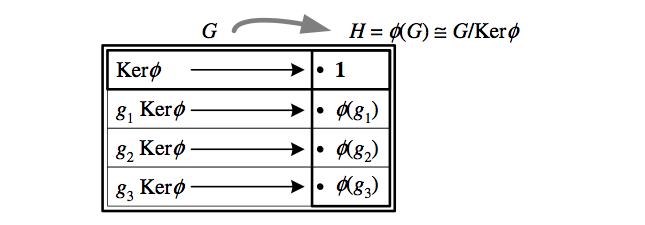
In general, \({\phi\left(G\right)\cong G/\textrm{Ker}\phi}\) is not a subgroup of \({G}\), so we cannot use this equation to decompose \({G}\) into an internal product by “multiplying both sides by \({\textrm{Ker}\phi}\).” If \({H}\) is a subgroup of \({G}\) and there is a homomorphism \({\phi\colon G\to H}\) that is the identity on \({H}\), we can once again extend the arithmetic of groups to state that \({G=\textrm{Ker}\phi\rtimes H}\), where \({\rtimes}\) represents the semidirect product (sometimes stated “\({G}\) splits over \({\textrm{Ker}\phi}\)”).

Note that the semidirect product as defined here is an internal product formed from \({G}\), and is distinct from the direct product since in general \({(n_{1}h_{1})(n_{2}h_{2})\neq(n_{1}n_{2})(h_{1}h_{2})}\); in fact non-isomorphic groups can be the semidirect products of the same two constituent groups. If \({H}\) is normal as well as \({N}\), then this is not the case and the semidirect product is the same as the internal direct product.

An equivalent definition of the semidirect product starts with a normal subgroup \({N}\) of \({G}\), defining \({G=N\rtimes H}\) if \({G=NH}\) and \({N\cap H=\mathbf{1}}\), or equivalently if every element of \({G}\) can be written in exactly one way as a product of an element of \({N}\) and an element of \({H}\). These properties can be seen in a common use of the semidirect product in physics, where \({N}\) is the group of translations in \({\mathbb{R}^{n}}\), \({H}\) is the group of rotations and reflections, and \({N\rtimes H}\) is thus the group of all rigid transformations.