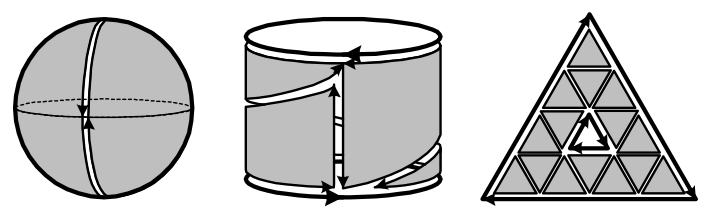
The point of introducing orientation is to use \({n}\)-chains to describe arbitrary \({n}\)-dimensional surfaces in \({X}\) composed of \({n}\)-simplices. By constructing such surfaces using adjacent simplices, internal boundaries can cancel when they consist of two boundaries in opposite directions. Constructing a surface out of simplices in this way is called a triangulation.

Many intuitive facts are accurately reproduced in this formal system, and extended to arbitrary dimension in a consistent way.