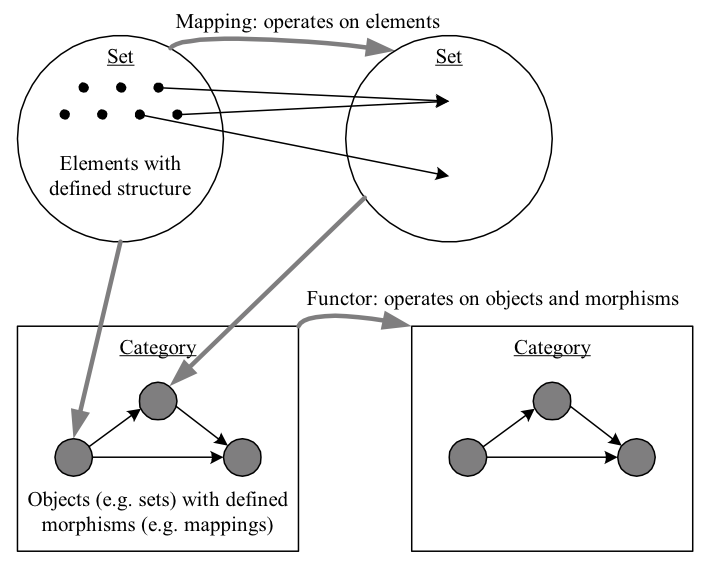
Recall the types of set mappings from the section on defining mathematical structures. It can be useful to generalize both sets and mappings, which takes us from set theory to category theory. Category theory eliminates any dependence upon elements, referring only to classes of generic objects. The class (AKA collection) of objects ${\textrm{ob}(C)}$ of a class ${C}$ sometimes may be defined as sets with a certain structure, but in category theory they are left completely abstract, with the following definitions built upon them:

• Morphisms: a set ${\textrm{mor}(X,Y)}$ (also denoted ${\textrm{hom}(X,Y)}$ or ${C(X,Y)}$) of morphisms between ${X}$ and ${Y}$ is defined for every ${X,Y\in \textrm{ob}(C)}$; every ${\textrm{mor}(X,X)}$ includes an identity ${\mathbf{1}_{X}}$
• Composition: an operator ${\circ}$ is defined between morphisms that is distributive and respects the identity, i.e. for morphisms ${m\colon X\to Y}$ and ${n\colon Y\to Z}$ we have ${n\circ m\colon X\to Z}$ with ${(n\circ m)\circ l=n\circ(m\circ l)}$ and ${m\circ\mathbf{1}_{X}=m=\mathbf{1}_{Y}\circ m}$

A category ${C}$ then consists of a class of objects ${\textrm{ob}(C)}$, a collection of sets of morphisms ${\textrm{mor}(X,Y)}$ between these objects, and a morphism composition operator. It is helpful in understanding these definitions to consider their application to sets and mappings. In this case, a class of objects would consist of sets along with a structure; morphisms would be mappings between these objects; and the category would consist of the class and the mappings.