Recall that on a differentiable manifold, it is not possible to use a tangent vector \({v}\) to “transport a point in the direction \({v}\)” in a coordinate-independent way, since there is no special curve on \({M}\) among the many that have \({v}\) as a tangent. On a Lie group this is possible, since the left-invariant vector fields provide a unique flow in the direction of \({v}\).

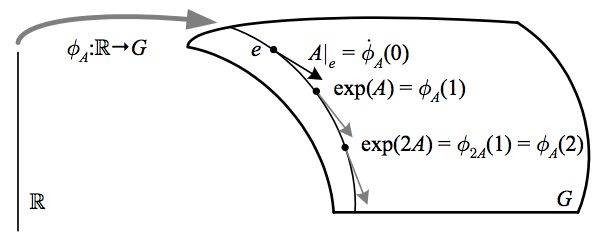
A one-parameter subgroup of \({G}\) is a homomorphism \({\phi\colon\mathbb{R}\to G}\). Given a left-invariant vector field \({A}\), there is a unique one-parameter subgroup \({\phi_{A}}\) such that \({\phi_{A}\left(0\right)=e}\) and \({\dot{\phi}_{A}\left(t\right)=A}\) for all \({t}\) (i.e. \({\phi_{A}\left(t\right)}\) is the local flow from the Lie derivative, but being defined for all \({t}\) it is called simply the flow of \({A}\)). We can then define the exponential map \({\textrm{exp}\colon\mathfrak{g}\to G}\) by

\(\displaystyle \mathrm{exp}(A)\equiv e^{A}\equiv \phi_{A}\left(1\right). \)

Since scaling the parametrization scales the tangent vectors, we have \({\phi_{A}\left(t\right)=\phi_{tA}\left(1\right)=\mathrm{exp}(tA)}\).

In particular, the elements of \({G}\) infinitesimally close to the identity can be written \({e+\varepsilon A}\). The exponential map is a generalization of familiar exponential functions: if \({G=\mathbb{R}^{+}}\), the positive reals under multiplication, \({\mathfrak{g}=\mathbb{R}}\) and \({\textrm{exp}}\) is the normal exponential function for real numbers; if \({G}\) is the non-zero complex numbers under multiplication, \({\mathfrak{g}=\mathbb{C}}\) and \({\textrm{exp}}\) is the normal complex exponential function; and if \({G=GL(n,\mathbb{R})}\), the real invertible \({n\times n}\) matrices under matrix multiplication, \({\mathfrak{g}=gl(n,\mathbb{R})}\), the real \({n\times n}\) matrices, and \({\textrm{exp}}\) is matrix exponentiation, defined by

\(\displaystyle e^{A}\equiv\overset{\infty}{\underset{k=0}{\sum}}\frac{1}{k!}A^{k}. \)

The multiplication of matrix exponentials does not follow the scalar rule, instead being given by the Baker-Campbell-Hausdorff formula:

\(\displaystyle e^{A}e^{B}\equiv e^{A+B+\frac{1}{2}\left[A,B\right]+\dotsb} \)

The terms that continue the series are all expressed in terms of Lie commutators, and as Lie brackets hold for the exponential maps of any Lie algebra; however, the series may not converge, limiting validity to a neighborhood of the identity. The terms shown above comprise the entire series if both matrices commute with the commutator, i.e. if \({\left[A,\left[A,B\right]\right]=\left[B,\left[A,B\right]\right]=0}\).