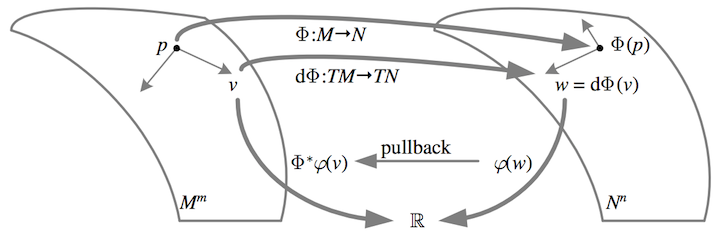
If we consider a general mapping between manifolds \({\Phi\colon M^{m}\to N^{n}}\), we can choose charts \({\alpha_{M}\colon M\to\mathbb{R}^{m}}\) and \({\alpha_{N}\colon N\to\mathbb{R}^{n}}\), with coordinate functions \({x^{\mu}}\) and \({y^{\nu}}\), so that the mapping \({\alpha_{N}\circ\Phi\colon M\to\mathbb{R}^{n}}\) can be represented by \({n}\) functions \({\Phi^{\nu}\colon M\to\mathbb{R}}\). This allows us to write down an expression for the induced tangent mapping or differential (aka pushforward, derivative) \({\mathrm{d}\Phi\colon TM\to TN}\) (also denoted \({T\Phi}\) or \({\Phi_{*}}\) or sometimes simply \({\Phi}\) if it is clear the argument is a tangent vector). For a tangent vector \({v=v^{\mu}\partial/\partial x^{\mu}}\) at a point \({p\in M}\) we define
\(\displaystyle \left.\mathrm{d}\Phi\left(v\right)\right|_{p}\equiv\left.v^{\mu}\frac{\partial\Phi^{\lambda}}{\partial x^{\mu}}\frac{\partial}{\partial y^{\lambda}}\right|_{\Phi\left(p\right)}. \)
This definition can be shown to be coordinate-independent and to follow our intuitive expectation that mapped tangent vectors stay tangent to mapped curves. If \({M=N}\) and \({\Phi}\) is the identity, \({\mathrm{d}\Phi}\) is just the vector component transformation from the previous section on tangent vectors. The matrix \({J_{\Phi}(x)\equiv\partial\Phi^{\nu}/\partial x^{\mu}}\) is called the Jacobian matrix (AKA Jacobian). For the parametrized curve \({C\colon\mathbb{R}\to N^{n}}\), we define the tangent to the curve at \({t\in\mathbb{R}}\) to be
\begin{aligned}\dot{C}\left(t\right) & \equiv\left.\mathrm{d}C\left(\frac{\partial}{\partial x}\right)\right|_{t}\\
& =\left.\frac{\partial C^{\lambda}}{\partial x}\frac{\partial}{\partial y^{\lambda}}\right|_{C\left(t\right)},
\end{aligned}
which is also denoted \({\mathrm{d}C\left(t\right)/\mathrm{d}t}\) and coincides with the Euclidean tangent to a curve if \({N=\mathbb{R}^{n}}\).
If \({\Phi}\) is a diffeomorphism, \({\mathrm{d}\Phi}\) is an isomorphism between the tangent spaces at every point in \({M}\). The inverse function theorem says that the converse is true locally: if \({\mathrm{d}\Phi_{p}}\) is an isomorphism at \({p\in M}\), then \({\Phi}\) is locally a diffeomorphism. In particular, this means that if in some coordinates the Jacobian is nonsingular, then \({\alpha_{N}\circ\Phi\circ\alpha_{M}^{-1}}\) represents a locally valid coordinate transformation and \({\Phi^{\nu}=y^{\nu}}\).
A mapping between manifolds \({\Phi\colon M^{m}\to N^{n}}\) also can be used to naturally define the pullback of a form \({\Phi^{*}\colon\Lambda^{k}N\to\Lambda^{k}M}\) by \({\Phi^{*}\varphi\left(v_{1},\dotsc,v_{k}\right)=\varphi\left(\mathrm{d}\Phi\left(v_{1}\right),\dotsc,\mathrm{d}\Phi\left(v_{k}\right)\right)}\), where the name indicates that a form on \({N}\) can be “pulled back” to \({M}\) using \({\Phi}\). Note that the composition of pullbacks is then \({\Psi^{*}\Phi^{*}\varphi=(\Phi\Psi)^{*}\varphi}\).
Note that for a mapping \({f\colon M\to\mathbb{R}}\), we have \({\mathrm{d}f\colon TM\to T\mathbb{R}\cong\mathbb{R}}\), so that \({\mathrm{d}f\left(v\right)=v^{\mu}\partial f/\partial x^{\mu}=v\left(f\right)}\), the directional derivative of \({f}\). Let us apply this to the coordinate function \({x^{1}\colon M\to\mathbb{R}}\). Then we have \({\mathrm{d}x^{1}\left(v\right)=v^{\mu}\partial x^{1}/\partial x^{\mu}=v^{1}}\), so that in particular \({\mathrm{d}x^{v}\left(\partial/\partial x^{\mu}\right)=\delta^{v}{}_{\mu}}\), i.e. \({\mathrm{d}x^{\mu}}\) is in fact the dual frame to \({\partial/\partial x^{\mu}}\). Thus in a given coordinate system, we can write a general tensor of type \({(m,n)}\) as
\(\displaystyle T=T^{\mu_{1}\dots\mu_{m}}{}_{\nu_{1}\dots\nu_{n}}\frac{\partial}{\partial x^{\mu_{1}}}\otimes\dotsb\otimes\frac{\partial}{\partial x^{\mu_{m}}}\otimes \mathrm{d}x^{\nu_{1}}\otimes\dotsb\otimes \mathrm{d}x^{\nu_{n}}. \)
In particular, the metric tensor is often written
\(\displaystyle {\mathrm{d}s^{2}\equiv g=g_{\mu\nu}\mathrm{d}x^{\mu}\mathrm{d}x^{\nu}}, \)
where the Einstein summation convention is used and the tensor symbol omitted. A general \({k}\)-form \({\varphi\in\Lambda^{k}M}\) can then be written as
\(\displaystyle \varphi=\underset{\mu_{1}<\dotsb<\mu_{k}}{\sum}\varphi_{\mu_{1}\dots\mu_{k}}\mathrm{d}x^{\mu_{1}}\wedge\dotsb\wedge \mathrm{d}x^{\mu_{k}}. \)
From either the tangent mapping definition or the behavior of the exterior product under a change of basis, we see that under a change of coordinates we have
\(\displaystyle \mathrm{d}y^{\mu_{1}}\wedge\dotsb\wedge\mathrm{d}y^{\mu_{k}}=\textrm{det}\left(\frac{\partial y^{\nu}}{\partial x^{\mu}}\right)\mathrm{d}x^{\mu_{1}}\wedge\dotsb\wedge\mathrm{d}x^{\mu_{k}}. \)
This is the familiar Jacobian determinant (like the Jacobian matrix, also often called the Jacobian) that appears in the change of coordinates rule for integrals from calculus, and explains the name of the volume form as defined previously in terms of the exterior product.
In summary, the differential \({\mathrm{d}}\) has a single definition, but is used in several different settings that are not related in an immediately obvious way.
| Construct | Argument | Other names | Other symbols |
|---|---|---|---|
| \({\mathrm{d}\Phi\colon TM\to TN}\) | \({\Phi\colon M\to N}\) | Tangent mapping | \({T\Phi}\), \({\Phi_{*}}\), \({\Phi}\) |
| \({\mathrm{d}f\colon TM\to\mathbb{R}}\) | \({f\colon M\to\mathbb{R}}\) | Directional derivative | \({v\left(f\right)}\), \({\mathrm{d}_{v}f}\), \({\nabla_{v}f}\) |
| \({\mathrm{d}x^{\mu}\colon TM\to\mathbb{R}}\) | \({x^{\mu}\colon M\to\mathbb{R}}\) | Dual frame to \({\partial/\partial x^{\mu}}\) | \({\beta^{\mu}}\) |