For algebraic objects, the most basic structure-preserving map was a homomorphism. The most basic equivalence in topology is the similarly named homeomorphism. Homeomorphic spaces are “the same” from a topological point of view.
| ◊ One can visualize a homeomorphism as stretching and bending a space arbitrarily, since length and curvature involve structure beyond open sets and so are “invisible” from the topological viewpoint. |
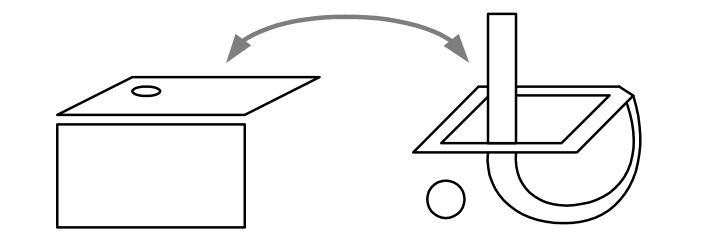
There exists an even looser equivalency in topology, called a homotopy equivalency. The essential conceptual difference is that since it is bijective, a homeomorphism preserves the dimensionality of the object while stretching and bending, while a homotopy equivalency allows the collapse of dimensions, while still preserving holes.
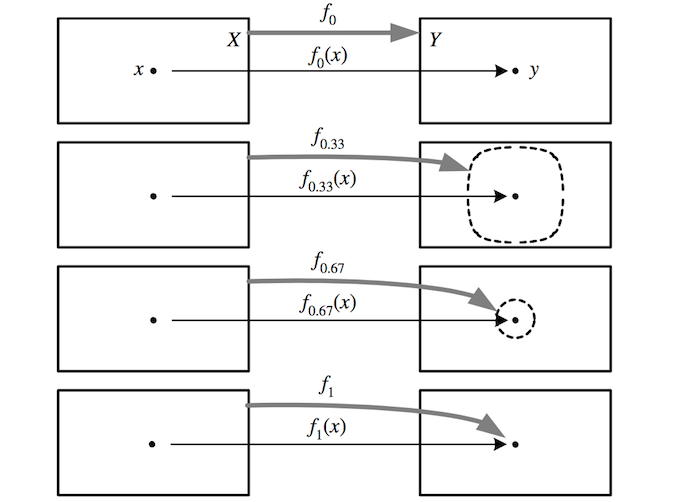
To make this concept precise, we first define a homotopy between spaces, a continuous family of continuous maps \({f_{t}\colon X\to Y;}\) i.e. \({f}\) is continuous when considered as a function of \({t}\) as well as when considered as a function of points in \({X}\). Two maps are homotopic if there is a homotopy between them, i.e. \({f_{0}}\) is homotopic to \({f_{1}}\) if \({t}\) runs from 0 to 1.
The above depicts a homotopy \({f_{t}}\) from \({X}\) to \({Y}\); the map \({f_{0}}\) onto \({Y}\) is homotopic to the map \({f_{1}}\) which maps all of \({X}\) to a point \({y}\).
A couple of related definitions are:
- Homotopy relative to \({A}\) (denoted homotopy rel \({A}\)): a homotopy that is independent of \({t}\) on \({A\subset X}\); e.g. in the above figure \({f_{t}}\) is a homotopy rel \({x}\)
- Deformation retraction from \({X}\) to \({A}\): a homotopy rel \({A}\) from the identity to a retraction from \({X}\) to \({A}\); e.g. if we take \({Y=X}\) and \({y=x}\) above, \({f_{t}}\) is a deformation retraction from \({X}\) to \({x}\)
The precise definition of two spaces being homotopy equivalent, or having the same homotopy type (denoted \({X\simeq Y}\)), is not important for our purposes; instead, we will state the derived fact that \({X\simeq Y}\) iff they are deformation retracts of the same space. A space homotopy equivalent to a point is then called contractible.
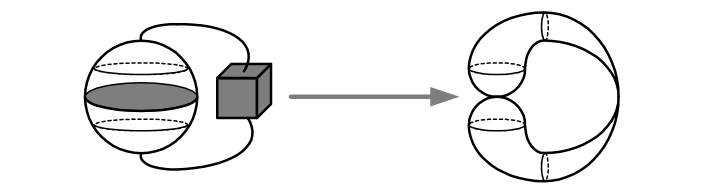
The above depicts a deformation retraction that collapses the equatorial disc inside the sphere, the strings, and the solid cube to points; the two spaces are thus homotopy equivalent.
| ◊ Homotopy equivalency can be viewed as meaning that we can collapse or expand any parts of the space as well as bending and stretching. |